ARKUSZ MATURALNY 2012 Alkain: Proszę o nie pisanie zbytnio w tym temacie tylko o rozwiązanie podanych zadań, aby każdy zobaczył jak to należało zrobić. http://www.cke.edu.pl/images/stories/00000000000000002012_matura2012/matematyka_pr.pdf

kylo1303: Zadanie 1 n, n+1 , n+2 n+3 , n∊C n+3=n²+(n+2)² + (n+1)² n+3=3n²+6n+5 3n²+5n+2=0 n₁=−1

	2
n2=−		Nie nalezy do dziedziny
	3

n=−1 n+1=0 n+2=1 n+3=2

Alkain: zad.1 x²+(x+1)²+(x+2)²=x+3 x²+x²+2x+1+x²+4x+4=x+3 3x²+5x+2=0 Δ=25−4*3*2 Δ=1

	−2
x1=
	3

x₂=−1 a=−1 b=0 c=1 d=2

Alkain: zad.7. Wiadoma a+b≥0 a³+b³≥a²b+ab² a³−a²b+b³−ab²≥0 −a²(−a+b)+b²(b−a)≥0 (b−a)(b²−a²)≥0 (b−a)(b−a)(b+a)≥0 (b−a)²(b+a)≥0 Komentarz kwadrat dowolnej liczby jest dodatni z założenia wiemy ze a+b≥0 więc całość większa bądź równa 0

kylo1303: Zadanie 8 12=2*2*3=2*6=3*4 1^o {1,1,1,1,1,1,3,4} z tych liczb mamy: |A|=7*8=56 2^o {1,1,1,1,1,1,2,6} z tych liczb mamy: |B|=7*8=56 3^o {1,1,1,1,1,2,2,3} z tych liczb mamy:

	8 2
|C|=		*6=7*8*3=168

Wszystkich jest wiec: |N|=56+56+168=280

Alkain: zad.2. x⁴+x²−2x≥0 x(x³+x−2)≥0 x₁=0 w(x)=x³+x−2 w(1)=0 x₂=1 x³+x−2 dzielimy przez (x−1) Wychodzi nam w(x)=(x²+x+2)(x−1) Całość x(x−1)(x²+x+2)≥0 Miejsca zerowe 1 i 0 wartości większe wprzedziałach (−∞,0>u<1,∞)

Alkain: Ktoś robi jakieś zadanie ?

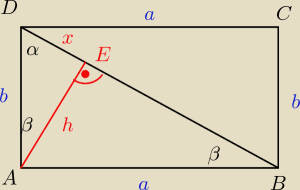
kylo1303: |BD|²=a²+b² |BD|=√a²+b² |DE|=x

	1		1
PABD=		ab=		*|BD|*h
	2		2

	ab
h=
	√a2+b2

Trojkaty ADE i ABD sa podobne (wszystkie katy takie same)

x		b
	=
h		a

	b		ab		b2
x=		*		=
	a		√a2+b2		√a2+b2

	1		1		b2		ab		ab3
PAED=		*x*h=		*		*		=
	2		2		√a2+b2		√a2+b2		2*(a2+b2)

TOmek: robie 4.

Alkain: To ja 3.

asdf: x⁴ + x² − 2x ≥ 0 x(x³ + x − 2) ≥ 0 x(x³ + x − 1 − 1) ≥ 0 x((x³ − 1) + 1(x − 1))≥ 0 x((x − 1)(x² + x + 1) + 1(x − 1)) ≥ 0 x(x − 1)(x² + x + 2)≥ 0 to też jest dobrze??

Alkain: zad.3. cos2x+2=3cosx gdzie cos2x=cos²x−sin²x (sin²x=1−cos²x) cos2x=2cos²x−1 2cos²x−1−3cosx+2=0 cosx=t 2t²−3t+2=0 Δ=9−4*2*1 Δ=1 t₁=1

	1
t2=
	2

t₁=cosx=1 dla x=2kπ gdzie k∊c

	1		π
t2=cosx=		dla x=		+2kπ gdzie k∊C v
	2		3

	π
x=−		+2kπ gdzie k∊C
	3

Alkain: asdf sądzę że tak

TOmek: założenia 1^oΔ>0 2^ox₁⁴+x₂⁴=4m³+6m²−32m+12 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 1^o Δ=(x−√12)(x+√12>0 x∊ (−∞,√12) u (√12,∞) −−−−−−−−−−−−−−−−−−−−−−−−−−−−− 2^o x⁴+x⁴=(x₁²)²+(x₂²)²=(x₁²+x₂²)²−2(x₁*x₂)² rozpisuje: x₁²+x₂²=(x₁+x₂)²−2x₁*x₂ i wstawiam do góry ((x₁+x₂)²−2x₁*x₂ )²−2(x₁*x₂)² −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− wzóry Vieta x₁+x₂= m+2 x₁*x₂=m+4 −−−−−−−−−−−−−−−−−−−− ((m+2)²−2(m+4) )²−2(m+4)²= (m²+4m+4−2m−8)²−2(m²+8m+16)= (m²+2m−4)²−2m²−16m−32= ((m²+2m)−(4))²−2m²−16m−32= (m²+2m)²−2*4*(m²+2m)+16−2m²−16m−32 m⁴+4m³+4m²−8m²−16m+16−2m²−16m−32= 2 załozenie : m⁴+4m³−6m²−6m−16=4m³+6m²−32m+12 −3m⁴−12m²−28=0 −3t²−12t−28=0 t≥0 /// gdzieś tu mam błąd w obliczeniach, ale nie mam juz głowy by go znaleźc wynik to: m=−√14, p{14] co spełnia warunek 1^o i jest odpowiedzią.

Alkain: Tutaj chyba niedługo będą odpowiedzi, więc nie wiem cy jest sens robić dalej... http://www.edulandia.pl/matura/1,118553,11686688,Matura_2012__matematyka__poziom_rozszerzony___odpowiedzi.html